Eyeglasses & Optics

Eyeglasses consist of specially ground spectacle lenses, placed into frames to wear on the face.  The lenses are prescribed and ground to specific standards.  These lenses are convex on the front surface and concave on the back surface.

Typically, eyeglass lenses compensate for the refractive error of a person’s eyes, enabling that person to see more clearly far away, at near, or both.  Such lenses usually are prescribed to compensate for a refractive error (myopia, hyperopia, and/or astigmatism) as well as for presbyopia.  They also can be prescribed with a prismatic correction to compensate for an extraocular muscle imbalance, such as a phoria or a strabismus that is not too great.

The back surface of a spectacle lens is concave for optical reasons.  For one thing, when the eye moves around, it will be about the same distance from the back of the lens if it is concave, but the eye-lens distance would vary more if the back lens surface were convex.  Also, there are less aberrations and distortion, and better optical quality, with front/convex and back/concave surfaces on a lens.

In addition, a concave back lens surface conforms more naturally to the convex curvature of the face.  An added bonus is that the eyelashes are less likely to rub against the back surface of a lens if it is concave than if it is convex.

With better technology in edging equipment, an aspheric curve can be ground more accurately into one or both surfaces of prescription lenses, providing better visual clarity.  Digital surfacing allows a plastic blank to be molded very precisely to achieve the best cosmetic result and correct optical power.

frames

Probably the oldest eyeglass frames known are recorded in a painting by di Modena in 1352.  These were represented as two lenses set in metal rims and joined together centrally.

After many years, metal frames were replaced by leather rims.  In order to avoid the tiring necessity of holding up the glasses rims manually, they often were tied by a tape inserted under one’s hat.

Lornettes soon appeared to aid the support of eyeglasses.  However, it was not until the latter part of the 19th century that temple pieces were used on eyeglass frames.  Soon thereafter, frames with springs in their nosepieces were introduced.

About this time, a variety of materials such as gold, silver, horn, fishbone, wood, and steel were introduced in the manufacturing of eyeglass frames.  Today, scientific materials are employed that are lightweight, non-reactive, long-lasting, and comfortable.

diopters and focal length

The power or strength of a lens is measured in diopters (D).  The reciprocal (inverse) of the dioptric power of a lens equals the focal length, in meters, of the lens.  A “plus” lens converges light.  A “minus” lens diverges light.

For instance, consider a convex or converging (plus) lens with a power of +1.50 D (see illustration below).  The focal length, f, of that lens will be:

f = 1 ÷ +1.50 D = 0.667 meter = 66⅔ centimeters.

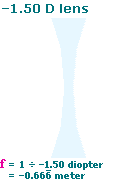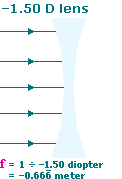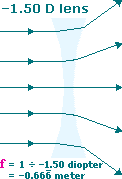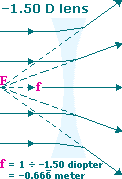
Now, consider a concave or diverging (minus) lens with a power of –1.50 D (see illustration below).  The focal length, f, of that lens will be:

f = 1 ÷ –1.50 D = –0.667 meter = –66⅔ centimeters.

Convex Lens forms a Real Image at F		Concave Lens forms a Virtual Image at F
If the two animations are not synchronized, reloading the page may help.

Obviously, the convex and concave lenses above would not work as eyeglass lenses.  Lenses worn in eyeglass frames are convex on the front surface and concave on the back surface.

Below are depictions of two spectacle or eyeglass lenses:

• a “plus” spectacle lens, which is thicker in the middle than on the edges, and
• a “minus” spectacle lens, which is thicker on the edges than in the middle.

Plus-Power Spectacle Lens

Minus-Power Spectable Lens

A plus lens compensates for hyperopia (farsightedness), while a minus lens compensates for myopia (nearsightedness).

spherocylinder prescription

A lens prescription typically includes both a sphere (or spherical) component and a cylinder (or cylindrical) component.  This known as a spherocylinder (or spherocylindrical) prescription.

The following is the typical format of a spherocylinder spectacle (glasses) prescription, written in “minus cylinder” form:

1. the first number is the sphere or spherical component,
2. the second number is the cylinder or cylindrical component, and
3. the third number is the axis or axis of astigmatism component.

For OD, +1.25 D is the power of the lens in the 15° meridian, while +1.25 D – 0.75 D = +0.50 D is the power of the lens 90° away, in the 105° meridian. 

For OS, –0.50 D is the power of the lens in the 85° meridian, while –0.50 D – 0.50 D = –1.00 D is the power of the lens 90° away, in the 175° meridian.

Here are “optical crosses” portraying the dioptric powers in the major meridians for each lens:

sphere

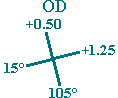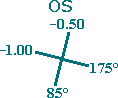The sphere or spherical component of a spectacle prescription indicates the degree of hyperopia (farsightedness) or myopia (nearsightedness) in the axis meridian of an eye.  While plus (+) power indicates hyperopia, minus (–) power indicates myopia.

In the case where there is no cylinder component of a lens prescription (indicating that the eye has no astigmatism, or maybe that the doctor has chosen not to compensate for the astigmatism, in that eye, with the glasses), there is only a sphere component to the prescription.  For instance, if there were no cylinder power in the above prescription, it commonly would be written as follows:

cylinder

The cylinder or cylindrical component of a spectacle prescription is an indication of the amount of astigmatism in an eye.  Astigmatism is the amount that the refractive structures of the eye (primarily, the front and back surfaces of the cornea and the front and back surfaces of the crystalline lens) vary or deviate from sphericity or a spherical shape.  That is, astigmatism indicates the degree of toricity or cylindrical shape of all of the eye’s refractive components, combined.

Keep in mind that the power or strength of a glasses prescription is opposite to the power of the eye itself, since the power of the glasses plus the power of the eye equals zero.  This means that, ideally, the light from a far away object passing through the glasses, and then entering a non-accommodating eye, will be focused on the retina.  It is in this way that the glasses “compensate” for the eye’s refractive error.

Therefore, the powers of the two eyes for which the compensating glasses above would be worn are as follows:

equivalent sphere

The equivalent sphere power of a lens prescription is the average of the dioptric powers, in all meridians, of a lens.  To obtain this value, add half of the cylinder power to the sphere power.  In other words, do the following:

1. Divide the cylinder power by 2.
2. Add this value to the sphere power.
3. The result is the equivalent sphere power of the lens.

,

OD: +1.25 D + (–0.75 D ÷ 2) = +1.25 D – 0.375 D = +0.875 D
OS:  –0.50 D + (–0.50 D ÷ 2) = –0.50 D – 0.25 D = –0.75 D.

“minus cylinder” vs. “plus cylinder”

An alternate way to write a spherocylinder prescription, which is equivalent to and equally correct with the “minus cylinder” form, is the “plus cylinder” form.  To convert from minus cylinder to plus cylinder form, or visa versa, do the following:

1. Add the sphere and cylinder powers together; this becomes the new sphere power.
2. Change the sign of the cylinder power, from minus (–) to plus (+), or from plus (+) to minus (–).
3. Change the axis value by 90°, remembering that the axis must be a number from 1 to 180.

Return to the Main Page
of Anatomy, Physiology & Pathology of the Human Eye